Simulaciones

Los trabajos computacionales desarrollados con el objetivo de simular un determinado modelo de un sistema particular son muy utilizados en la investigación científica, y en la física en particular. Podría decirse que su presentación en sociedad en gran escala se remonta al Proyecto Manhattan, con una simulación diseñada para modelar el proceso de detonación de una bomba nuclear (no siempre los conocimientos científicos se usan racionalmente).

Hay diversos tipos de simulaciones computacionales. La característica común que todos ellos comparten es el intento de generar un conjunto de escenarios representativos para un modelo, cuando la enumeración de todos los estados posibles del modelo se vuelve prohibitiva. En general cuentan con un número determinado de parámetros que pueden ser variados y permiten entonces estudiar el comportamiento de dicho sistema ante distintas características y condiciones iniciales.

En la educación se suelen utilizar simulaciones de entrenamiento, que en muchos sentidos equiparan y aun superan las ventajas de los videos educacionales, como los presentados antes. En particular porque permiten la interacción directa entre el docente y los alumnos con el “sistema simulado”. Por ejemplo, es posible realizar una animación sencilla que simule el movimiento de un vehículo bajo la acción de una cierta fuerza, dando la posibilidad de variar tanto las características del vehículo como la de la fuerza en cuestión, con un sencillo cambio de un par de parámetros. Esto se puede realizar de manera muy visual, permitiendo la obtención de resultados en tiempo real.

Una de las ventajas de las simulaciones es la de proporcionar experiencias estimulantes para los alumnos, incitándolos a realizar investigación. Además pueden ser útiles para auxiliar a los estudiantes a resolver los inconvenientes que suelen tener para comprender las diversas formas en que solemos representar a los sistemas físicos. Una animación puede ayudar a encontrar relaciones entre ellas y a construir modelos mentales de los sistemas. Por ejemplo, simulaciones que permiten a los estudiantes variar los parámetros de un sistema que responde a una determinada ecuación y observar el efecto que se obtiene, son extremadamente ventajosas para apreciar la relación entre las ecuaciones de la física y las magnitudes observadas.

Existe una gran cantidad de simulaciones para física (o animaciones) en la red, la mayoría de ellas en formato de applets (de application-let), componentes de software que corren en el contexto de otro programa, en general un navegador de internet. La ventaja de este formato es que permite realizar sencillas simulaciones de interés en la educación científica en muy pequeños programas visuales que ofrecen una interacción sencilla con el usuario y pueden ser rápidamente descargados. Muchos sitios ofrecen la fuente de estos applets, de tal forma que no es necesario estar on-line durante el desarrollo de la clase. En algunos casos, con un poco de entrenamiento es posible realizar modificaciones sobre ellos según las necesidades propias del docente.

Presentamos aquí algunas de ellas, como claros ejemplos de la potencialidad del uso de estas simulaciones. Los tres ejemplos que mostramos fueron realizados por F. Esquembre, Martín, W. Christian y M. Belloni y forman parte del libro FISLETS: enseñanza de física con material interactivo, publicado por Pearson Education. Los fislets (por Applets de Física) son propiedad de Wolfang Christian, del Davison College, y pueden ser descargados libremente del sitio http://webphysics.davidson.edu/Applets/Applets.html

El primer ejemplo lo constituye el de la colisión de dos carritos que cuentan con imanes en sus extremos para permitir que los móviles colisionen sin tocarse cuando se acercan (realizando el mismo papel que cumpliría un resorte). El applet permite variar (dentro de un rango limitado) las velocidades iniciales de los carritos y la masa de uno de ellos. De esta forma es posible reproducir colisiones bajo distintas condiciones y observar el resultado de las mismas. El objetivo principal de esta simulación es estudiar qué sucede con las energías involucradas. En particular, el gráfico superior muestra la evolución de la energía cinética de ambos móviles con el tiempo, mientras que las barras de la derecha representan la energía de cada uno de los carritos en un determinado instante, para simplificar la visualización. Es un buen ejemplo para hacer notar que la energía cinética total del sistema antes y después de los choques es la misma, pero que esto no sucede durante el momento en que se efectúa la colisión. Justamente el “tiempo” durante el cual tiene lugar la interacción puede ser definido en esta simulación, utilizando el diagrama superior, como aquel durante el cual se produce la transición de una velocidad inicial a otra final. En ese caso la energía cinética faltante se ha transformado en energía magnética, por lo que la energía total sí es una cantidad conservada a lo largo de toda la experiencia.

Otra aplicación particularmente interesante es la que permite representar el campo eléctrico de una determinada distribución de cargas. Estas pueden ser colocadas en cualquier posición, permitiendo armar distintas configuraciones (como dipolos y cuadrupolos). El campo eléctrico está representado por un vector que apunta en dirección del campo y con un color que representa su intensidad (blanco, azul, verde, rojo y negro en orden creciente de magnitud). La fuerza sobre una carga dada, esto es la suma de las fuerzas ejercidas por las otras cargas presentes, también es representada en este applet por el vector correspondiente.

Esta aplicación resulta muy práctica en una clase sobre campos eléctricos: intentar reproducir con cierto grado de fidelidad las líneas de campo en el pizarrón, aun en el caso de las configuraciones más sencillas, puede tornarse muy complicado. Aun contando en clase con una única computadora este applet es de gran utilidad, aunque ciertamente la situación ideal es la de permitir a los estudiantes interactuar directamente con el programa armando sus propias configuraciones.

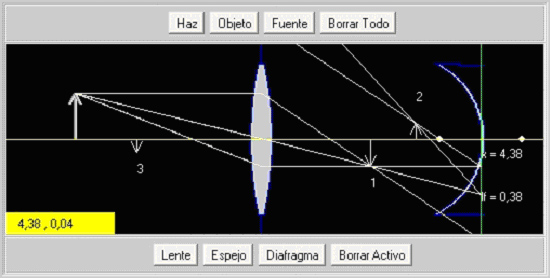
Como último ejemplo, ilustramos el referente a la óptica de lentes delgadas. Esta aplicación permite incorporar diversos componentes en el marco de un banco óptico: lentes delgadas, espejos, diafragmas, objetos, haces y fuentes puntuales de luz. El applet muestra entonces el resultado de la configuración armada, incorporando las imágenes de los objetos y trazando los “rayos” correspondientes. La distancia focal de lentes y espejos puede ser fácilmente modificada, permitiendo por ejemplo transformar lentes convergentes en divergentes y viceversa. Esta aplicación resulta útil tanto en combinación con clases explicativas sobre el tema como para facilitar el armado de una experiencia directa en el laboratorio.

Existe además un gran número de simulaciones que presentan problemas a ser resueltos por los alumnos. En algunos casos se trata de soluciones del tipo multiple-choice donde el alumno debe elegir la respuesta que considera correcta, por ejemplo para el diagrama de fuerzas de cuerpo libre de un determinado sistema. En otros se presenta algún sistema físico, por ejemplo un circuito eléctrico, donde se conocen todos los parámetros salvo uno, que debe ser obtenido resolviendo alguna ecuación conocida. Este caso es un interesante estímulo para que el alumno resuelva problemas que en general le resultan poco atractivos en su presentación usual.

En resumen, los videos y las simulaciones pueden resultar complementos muy interesantes de las clases teóricas y de laboratorio. En el caso de no existir un aula de computación, es decir un aula donde haya una computadora por cada dos o tres alumnos, pueden utilizarse básicamente como demostraciones. En el aula de computación es posible utilizar los applets como elementos de aprendizaje directo y/o para realizar evaluaciones.